Last October I posted an excerpt from a probability text demonstrating how the Infinite Monkey Theorem, which is often cited as an example of how chance can be both a causal agent and a plausible explanation for the origin of information, is not particularly meaningful (given what we now know about the Universe being finite). The excerpt ends with a reference to another “more controversial” example from the same text (Roberts, Richard A. “Independence and Repeated Trials.” An Introduction to Applied Probability, Addison-Wesley, 1992, pp. 89–91), which I promised to post as well. So here it is ….
Example 3.5.3
In 1953, two important scientific discoveries were reported. In England, James Watson and Francis Crick published their results on the structure of DNA, deoxyribose nucleic acid, the genetic code of life. In Chicago the same year, Stanley Miller and Harold Urey published results of their “origin of life” experiments in which they were able to produce amino acids from electrical energy and inorganic matter, i.e., chemicals. These two discoveries have subsequently been shown to be related through the theory of chemical evolution.
Chemical evolution is the evolution of first life from inorganic chemicals. In the scenario of chemical evolution, the first living cells are thought to have evolved from chemicals in a series of steps. The first step was the creation of the basic molecules needed to form proteins, DNA, RNA, and membranes. The first experiments of Miller and Urey were concerned with the formation of amino acids, the “building blocks” for proteins. These basic molecules are thought to have occurred in a “primordial soup” and, through repeated independent trials, to have formed into long chains to produce proteins, DNA, RNA, and other organic compounds needed by the first living cell. These organic molecules then combined to form a proto cell and, finally, the first living cell. In this example, we shall consider one aspect of chemical evolution, the chance formation of proteins from the amino acids that make up proteins in living cells. Thus we shall assume that all of the 20 different amino acids needed in protein synthesis were available as building blocks. Nineteen of the 20 amino acids needed in living cells occur in two forms, which we shall denote as left-handed and right-handed. They occur in approximately equal numbers. But only left-handed forms appear in living cells. Thus there are effectively 39 possible choices of amino acids–19 left-handed forms, 19 right-handed forms, and one amino acid that is neither.
An hypothesized mechanism by which these amino acids join together is “random,” i.e., repeated independent trials. The question is as follows. Is “chance,” i.e., the independent concatenation of amino acids, a reasonable mechanism for the appearance of first life? Let’s calculate the probability of forming one protein made up of 400 amino acids. A length of 400 is not, in fact, a large protein, but it is somewhat average.
To begin the calculations, let’s assume that the 20 different kinds of amino acids occur in equal numbers, i.e., 400/20 = 20 of each kinds in our hypothetical protein. Let’s perform the calculation in two steps. Suppose we assume that the correct kind of amino acid is selected for each of the 400 locations in our protein. “Chance” is required to select only left-handed (versus right-handed) forms. That is, what is the probability of selecting 380 left-handed forms from a 50/50 mixture of left- and right-handed forms? (We use 380 because one of the 20 kinds of amino acids occurs in one form only.) This probability is the same as the probability of 380 heads in 380 throws of a fair coin. Thus
 one protein, left versus right
one protein, left versus right![] = (1/2)^380 approx {10^-114.4}. ] = (1/2)^380 approx {10^-114.4}.](http://www.tinymoe.com/bigbookomaths/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_df81dd430c64770de25f95a3874ac359.png)
Now suppose both the sequence of amino acids and left-handedness are selected by “chance.” What is the probability of forming a single protein, 400 amino acids long, that is
 one protein
one protein![] = (1/2)^380(1/20)^400 approx {10^-635}? ] = (1/2)^380(1/20)^400 approx {10^-635}?](http://www.tinymoe.com/bigbookomaths/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_ac89339b6b835004759404fbc9191c79.png)
This is analogous to the probability of forming a specific sequence in one trial, i.e., the probability of event 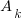 in Example 3.5.2.
in Example 3.5.2.
Now suppose we have a great number of trials N. What is the probability of formation in this case? If A is the event “form one protein,” then
![P delim{[}{A}{]} <= {N}/{10^635} P delim{[}{A}{]} <= {N}/{10^635}](http://www.tinymoe.com/bigbookomaths/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_978_7c47166be3e26c4d17c48cdf0e1634a7.png) , N = number of trials
, N = number of trials
by the same reasoning used in Example 3.5.2.
To create a large number of trials, let’s assume that every molecule in all the oceans on earth is an amino acid equally divided among the 39 forms. Assume that these amino acids link up in sets of 400 every millisecond for 10 billion years. What is the probability of forming a single protein in 10 billion years, that is
![P delim{[}{A}{]} <= {N}/{10^635} P delim{[}{A}{]} <= {N}/{10^635}](http://www.tinymoe.com/bigbookomaths/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_978_7c47166be3e26c4d17c48cdf0e1634a7.png) ?
?
The number of trials is
N =  .
.
And so,
![P delim{[}{A}{]} <= (10^65/400)/10^635 = 10^-590/400 <= 10^-590 P delim{[}{A}{]} <= (10^65/400)/10^635 = 10^-590/400 <= 10^-590](http://www.tinymoe.com/bigbookomaths/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_978_87df50e90248fb9dea8916d33768b1da.png) .
.
Thus any attempt to build a probabilistic model for protein formation, based on independent concatenation of amino acids, would assign probability zero to this event and discard independent trials as a plausible mechanism. “Chance” is not a reasonable mechanism to form a single average-length protein, much less all the other proteins, DNA, RNA, and membrane molecules needed to produce a living cell.
Some may argue that the entire 400-acid-long protein need not form in one simultaneous connection of 400 amino acids. Rather, the formation might occur with smaller units hooking up and then coming together in several steps. If the events of the amino acids coming together were independent, then it makes no difference how they are formed–whether in small chains or in one connection of 400. The probability of formation is the same.
Why should this example be controversial? The math is sound, basic, and almost self-explanatory, and it’s been reinforced over some 27 years since the publication of Roberts’ book (you can see some good related content here and here and here and here). To anyone who’s been paying attention, it’s clear that chemical evolution (and, I would argue, Darwinian Naturalism) has been fatally discredited as a valid explanation for the origin of life.
I think Roberts called this example “controversial” either because most people have not been paying attention or they’re bothered not by the evidence but rather by the implications of the evidence.
Because those implications are objectively moral and contradict the sacred credos of postmodernism, the controversy is therefore philosophical, not scientific (as Roberts noted).
More on that later ….
